НЕКОТОРЫЕ АПРИОРНЫЕ ОЦЕНКИ ДЛЯ РЕШЕНИЙ МНОГОМЕРНОЙ СМЕШАННОЙ ЗАДАЧИ ДЛЯ ОДНОГО КЛАССА НЕЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ТРЕТЬЕГО ПОРЯДКА
Authors
Aliyev Samed Jahangir oqlu,, Aliyeva Arzu Qambar qizi
Rubric:Mathematics
554
2
Share
554
2
Annotation
Some a priori estimates in
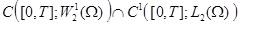
is obtained for all the possible almost everywhere solutions of a multidimensional mixed problem under consideration.
Keywords
mixed problem
non-linear differential equation
a priori estimate
Authors
Aliyev Samed Jahangir oqlu,, Aliyeva Arzu Qambar qizi
Rubric:Mathematics
554
2
Share
554
2
References:
- Алиев С.Дж. О существовании в малом и единственности в целом решения почти всюду многомерной смешанной задачи для одного класса нелинейных дифференциальных уравнений третьего порядка. I // Вестник БГУ, серия физико-математических наук, 2003, №3, с.36-42.
- Алиев С.Дж. О глобальном существовании решения почти всюду многомерной смешанной задачи для одного класса нелинейных дифференциальных уравнений третьего порядка. II // Вестник БГУ, серия физико-математических наук, 2003, №4, с.35-43.
- Aliyev S.J., Aliyeva A.Q. The study of multidimensional mixed problem for one class of third order semilinear psevdohyperbolic equations // European Journal of Pure and Applied Mathematics, 2017, v.10, No5, p.1078-1091.
- Beckenbach E., Bellman R. Inequalities, Mir, 1965, 276 p.
- Худавердиев К.И., Алиев С.Дж. Многомерная смешанная задача для одного класса полулинейных псевдогиперболических уравнений третьего порядка. Баку: Азтехуниверситет, 2012, 252 с.
Other articles of the issue
